- KAIST 물리학과 안재욱 교수 연구팀, 글로벌 공동연구 통해 양자 자성체 설명
- 하이젠베르크 모델의 극단적 이방성을 양자 시뮬레이션으로 구현하는 데 최초 성공
- 향후 양자물질 설계 및 초정밀 차세대 공학에 응용
 |
| (왼쪽부터) KAIST 물리학과 안재욱 교수, 물리학과 김강흔 대학원생, 코펜하겐 대학 클라우스 뭴머 교수, 덴마크 오르후스~.j |
최근 양자컴퓨터를 이용하는 물성 연구가 활발해지고 있다. 이는, 양자역학적으로 상호작용하는 물질을 연구하거나 설계할 때 기존의 컴퓨터를 이용한 계산은 근본적인 한계를 가지기 때문이다. 양자계의 경우 양자 얽힘 등의 효과로 인해 계산량이 기하급수적으로 증가하기 때문이다. 따라서 양자물질 설계를 위해 물질의 특성을 알아내고자 할 때, 양자컴퓨터를 이용하는 양자 시뮬레이션이 필요하다.
KAIST 물리학과 안재욱 교수 연구팀이 코펜하겐 대학 클라우스 뭴머(Klaus MØlmer) 교수 연구팀과 함께 양자 시뮬레이션을 수행하는 양자 컴퓨터 플랫폼으로 최근 가장 주목을 받는 리드버그 원자 양자 컴퓨터를 이용해 양자 자성체의 극단적 특성을 구현하는데 성공했다고 밝혔다.
자성체 물질은 하드 디스크와 같은 전자제품을 비롯해 전력 발전 등에도 사용되는 등 현대 기술의 핵심 요소다. 최근에는 상온 자성체를 넘어서 양자적 특성이 두드러지는 초저온에서 양자 자성체 특성에 관한 연구가 활발히 이뤄지고 있다. 초저온에서 수행되는 물성 분석 및 계측 연구는 MRI 등의 의학 기기 등에 응용될 뿐만 아니라, 차세대 초정밀 제어계측공학을 촉발할 것으로 기대된다.
 |
| 그림 1. 실험 장비의 모식도와 스핀의 전파를 나타낸 모식도, 실험결과 |
유명 물리학자 리처드 파인만은 1983년 양자계의 특성을 인공적인 양자계로 모방해 연구하는 양자 시뮬레이션을 제안하였다. 인공적으로 모방한 양자계의 특성을 연구하면 기존 양자계의 특성을 알아낼 수 있다.
양자 시뮬레이션을 이용한 양자 자성체의 연구는 지난 10년간 세계 유수의 대학과 연구소에서 이뤄지고 있으며 이전까지 알려지지 않은 양자 물질의 특성들을 실험적으로 확인하는 성과를 보였다. 현재 양자 물질을 시뮬레이션하는 데 있어 중요한 이슈 중 하나는 극단적인 상황 속 양자 물질의 현상을 관찰하는 것이다.
한편 이와 같은 양자 시뮬레이션을 수행하는 양자 컴퓨터 플랫폼으로 최근 가장 주목을 받는 것은 리드버그 원자다. 리드버그 원자는 최외각 전자가 이온화되어 떨어지기 직전의 매우 높은 에너지를 머금고 있는 원자로, 일반 원자의 만 배 정도의 지름을 가지며 
(10의 24제곱)배 정도 더 큰 상호작용을 한다. KAIST 물리학과 안재욱 교수 연구팀은 최근 리드버그 원자를 이용해 최대 156큐비트급의 양자 컴퓨터 계산을 선보인 바 있다.
이번 연구에서 글로벌 공동연구팀은 리드버그 원자를 이용한 양자 컴퓨터를 이용해 양자 자성체를 설명하는 모형 중 하나인 하이젠베르크 모형*을 양자 컴퓨터로 모방해 구현했다. 특히 이전의 하이젠베르크 모형의 구현과 다르게, 이번 연구에서는 리드버그 원자의 강한 상호작용을 이용한 극단적 이방성 (3차원 중 특정 방향이 다른 방향 대비 1000배 이상 강하게 상호작용하는 특성으로 새로운 연구영역이 확보됨)을 구현하는 데 성공했다.
*하이젠베르크 모형: 하이젠베르크 자성체 모형은 자성체 스핀 간의 모든 방향 (x, y, z 방향) 상호작용을 가정한 모형으로 양자 자성체의 대표적 모델 중 하나임.
연구를 주도한 KAIST 물리학과 안재욱 교수는 “이번 연구는 리드버그 양자컴퓨터를 이용해 새로운 양자 물성을 연구할 수 있음을 보였다”라고 밝히고 “양자컴퓨터를 이용하는 물성 연구가 활발해질 것”이라고 기대했다.
KAIST 물리학과 김강흔 대학원생 연구원과 덴마크 오르후스 대학의 팬 양(Fan Yang) 박사후 연구원이 참여한 이번 연구는 국제 학술지 `피지컬 리뷰 X (Physical Review X)' 2월 14권에 출판됐다. (논문명 : Realization of an Extremely Anisotropic Heisenberg Magnet in Rydberg Atom Arrays). 한편 이번 연구는 삼성미래기술재단과 한국연구재단의 지원으로 수행됐다.
□ 연구 개요
연구 배경
양자계의 경우 양자 얽힘 등의 효과로 인해 계산량이 기하급수적으로 증가한다. 유명 물리학자 리처드 파인만은 이러한 문제를 해결하고자 1983년 양자컴퓨터를 이용한 양자 시뮬레이션을 제안한 바 있다. 이는 계산하고자 하는 물질의 특성을 양자컴퓨터로 모방해서, 이렇게 인공적으로 만든 양자계의 특성을 연구하여 원하는 물질의 특성을 알아내는 방식이다.
양자 시뮬레이션을 이용한 양자 자성체의 연구는 세계 유수의 대학과 연구소에서 이뤄지고 있으며 이전까지 알려지지 않은 양자 물질의 특성들을 실험적으로 확인하는 성과를 보였다. 현재 양자 물질을 시뮬레이션하는 데 있어 중요한 이슈 중 하나는 극단적인 상황 속 양자 물질의 현상을 관찰하는 것이다.
2. 연구 내용 상세
이번 KAIST 양자컴퓨터 연구는 리드버그 원자의 강한 상호작용을 이용하여 하이젠버그 자성체 모형을 실험적으로 계산하는 데 성공했다. 여기서 하이젠베르크 자성체 모형은 자성체 스핀 간의 모든 방향 (x, y, z 방향) 상호작용을 가정한 모형이다. 스핀은 3차원 공간 속 x, y, z 세 방향으로 놓일 수 있는데, 같은 방향으로 정렬된 스핀들끼리 각각 Jx, Jy, Jz의 상호작용을 가정할 때, 세 상호작용의 크기가 모두 같은 경우는 관습적으로 XXX 모형이라고 부르며, 두 개가 같을 경우 XXZ, 모두 다를 경우 XYZ 모형이라고 부른다. 이번 KAIST 연구는 하이젠베르크 XXZ 자성체 모형을 실험적으로 구현하였다.
KAIST가 구현한 하이젠베르크 XXZ 자성체 모형은 이전에는 볼 수 없었던 매우 강한 z 방향 상호작용(Jz)을 보여준다. 즉, 하이젠베르크 자성체의 극단적 이방성을 구현하는 데 성공했다. 이를 확인하는 실험으로 두 개의 이웃한 업 스핀 상태( 
)가 하나의 쌍으로 묶여 움직이는 것을 연구팀은 확인했다. 또한, 이전에 구현할 수 없었던 원거리 상호작용을 구현해 두 위치 떨어진 업 스핀 상태( 
)또한 하나의 쌍으로 묶여 움직이는 것을 확인했다.
또한, 이번 연구에서 두 이웃한 스핀이 시간이 지남에도 초기 위치에 얼어붙어 있는 결과(frozen dynamics)를 실험적으로 확인할 수 있었다. 이는 모든 양자 상태의 집합인 힐베르트 공간이 파편화될 수 있다는 실험적 증거가 된다. 참고로, 일반적인 스핀파가 전파될 때 스핀의 개수는 보존되며, 강한 z 방향 상호작용은 스핀 구역벽(domain wall), 즉 업 스핀과 다운 스핀 경계의 개수도 보존되다. 때문에, 두 보존 법칙으로 인해 스핀의 움직임이 제한되는 경우, 힐베르트 공간이 파편화되게 될 수 있으며, 이는 양자 통계 물리의 근간을 이루는 양자 에르고딕 정리(quantum ergodic theorem)의 반례 중 하나이다.
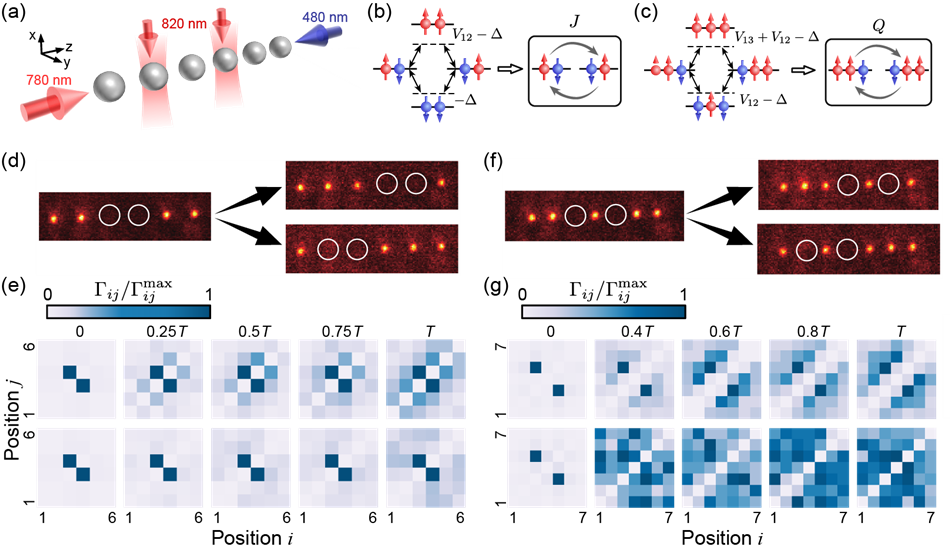
<그림 1> 실험 장비의 모식도와 스핀의 전파를 나타낸 모식도와 함께, 극단적 이방성을 가지는 하이젠베르크 모형의 시간에 따른 변화를 확인한 실험 결과이다. (a) 실험 장비의 모식도. (b) 하나의 스핀은 Jx Jy 상호작용을 통해 옆의 위치로 전파된다. (c) 두 이웃한 스핀은 극단적으로 강한 Jz 상호작용으로 인해 쌍으로 움직인다. (d) 이웃한 스핀쌍의 움직임을 실험한 사진. (e) 시간에 따른 이웃한 스핀쌍의 스핀 사슬의 위치와 스핀 밀도의 상관관계표. 특정 실험 조건에서는 스핀은 쌍으로 전파되는 반면 (위, 대각 상관관계), 다른 조건에서는 초기 위치에서 변화하지 않고 얼어버린다 (아래). (f) 하나 떨어진 스핀쌍의 움직임을 실험한 사진. (g) 시간에 따른 하나 떨어진 스핀쌍의 스핀 사슬의 위치와 스핀 밀도의 상관관계표. 특정 조건에서는 스핀은 쌍으로 전파되는 반면 (위, 대각 상관관계), 다른 조건에서는 개별 스핀이 독립적으로 움직이며 상관관계가 없어진다.
3. 기대 효과
이번 KAIST 연구는 리드버그 양자컴퓨터가 양자 자성체의 물리적 특성을 계산할 뿐만 아니라, 물리의 근본문제 중 하나인 양자 에르고딕 정리를 연구하는 데 활용될 수 있음을 보여준다. 이번 실험에서는 하이젠베르크 자성체의 극단적 이방성이 힐베르트 공간 파편화(Hilbert space fragmentation)에 이르는 실험적 가능성이 제시되었다. 여기서 힐베르트 공간 파편화는 최근 활발히 연구되고 있는 주제 중 하나로, 양자 다체계 흉터 (quantum many-body scar) 등과 함께 양자 통계 물리의 근간을 이루는 양자 에르고딕 정리(quantum ergodic theorem)의 반례 중 하나다.
참고로 양자 에르고딕 정리는 충분한 시간이 흐르면 초기 양자 상태가 변화하면서 같은 에너지를 가지는 모든 양자 상태를 한 번씩 거치며 양자 상태의 발견 확률은 열적 평형상태에 도달한다는 정리로, 고전 열 통계 물리학의 에르고딕 정리의 확장이다.)
KAIST 홍보실 제공
노벨사이언스 science@nobelscience.co.kr
<저작권자 © 노벨사이언스, 무단 전재 및 재배포 금지>
간단한 공정으로 이산화탄소 분리 성공
